Ռիմանի թեորեմը լոկալիզացիայի սկզբունքի մասին:
[խմբագրել]Դիցուք  ֆունկցիան ինտեգրելի է իսկական իմաստով կամ բացարձակ ինտեգրելի է անիսկական իմաստով
ֆունկցիան ինտեգրելի է իսկական իմաստով կամ բացարձակ ինտեգրելի է անիսկական իմաստով ![{\displaystyle [-\pi \;;\pi \;]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc409c7da7171825e301c33cbf345ea4c61ca42b) միջակայքում, ընդ որում`
միջակայքում, ընդ որում`  :
:  ֆունկցիայի Ֆուրյեի շարքի զուգամիտությունը և գումարի արժեքը կախված է հետևյալ սահմանից.
ֆունկցիայի Ֆուրյեի շարքի զուգամիտությունը և գումարի արժեքը կախված է հետևյալ սահմանից.
 :
:
Եթե այն գոյություն ունի, ապա Ֆուրյեի շարքի գումարը հենց դա է, ընդ որում`
 :
:
Մնացած կետերում արժեքները դեր չեն խաղում:
Ապացույց.
 ֆունկցիան պարբերական շարունակենք ամբողջ թվային առանցքի վրա:
Դիրիխլեյի ինտեգրալի մեջ կատարենք փոփոխականի փոխարինում`
ֆունկցիան պարբերական շարունակենք ամբողջ թվային առանցքի վրա:
Դիրիխլեյի ինտեգրալի մեջ կատարենք փոփոխականի փոխարինում`


|
Եթե տրված է  պարբերությամբ պարբերությամբ  ֆունկցիա, ապա. ֆունկցիա, ապա.
 : :
Ապացույց.
նշանակենք  : Կունենանք` : Կունենանք`
 : :
|
Հավասարության աջ մասը ներկայացնելով երկու ինտեգրալների գումարի տեսքով, առաջին ինտեգրալի մեջ կատարելով  փոփոխականի փոխարինում, և հաշվի առնելով Դիրիխլեյի կորիզի զույգությունը`
փոփոխականի փոխարինում, և հաշվի առնելով Դիրիխլեյի կորիզի զույգությունը`  , կստանանք`
, կստանանք`

 :
:
Ստացված արտահայտության մեջ տեղադրելով Դիրիխլեի կորիզի արժեքը, կստանանք`
![{\displaystyle S_{n}(x_{0},f)={1 \over \pi }\int \limits _{0}^{\pi }{\sin(2n+1){u \over 2}\cdot {{\left[{f(x_{0}+u)+f(x_{0}-u)}\right]} \over {2\sin {u \over 2}}}du}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b0174bd004d748cea6fd0bd781366bcaf415873) :
:
Այժմ ֆիքսենք որևէ  թիվ, և ստացված հավասարության աջ մասը ներկայացնենք երկու ինտեգրալների գումարի տեսքով`
թիվ, և ստացված հավասարության աջ մասը ներկայացնենք երկու ինտեգրալների գումարի տեսքով`
![{\displaystyle S_{n}(x_{0},f)={1 \over \pi }\int \limits _{0}^{\delta }{\sin(2n+1){u \over 2}\cdot {{\left[{f(x_{0}+u)+f(x_{0}-u)}\right]} \over {2\sin {u \over 2}}}du}+{1 \over \pi }\int \limits _{\delta }^{\pi }{\sin(2n+1){u \over 2}\cdot {{\left[{f(x_{0}+u)+f(x_{0}-u)}\right]} \over {2\sin {u \over 2}}}du}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48079a1d5daa92e5590537d4b9b48726c474fd0e) :
:
Քանի որ  ֆունկցիան անընդհատ է, և, հետևաբար, նաև սահմանափակ
ֆունկցիան անընդհատ է, և, հետևաբար, նաև սահմանափակ ![{\displaystyle \left[{\delta ,\pi }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f5d87b4c91639d829d98229c69ef2c231b08286) հատվածի վրա,
հատվածի վրա,
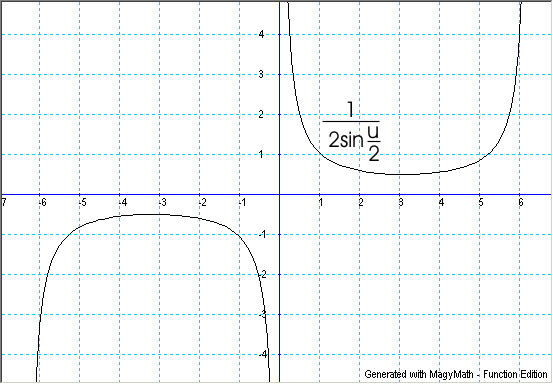
իսկ  ֆունկցիան` ցանկացած
ֆունկցիան` ցանկացած ![{\displaystyle x\in \left[{-\pi ;\pi }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32d26fb14f71309a583f8e22474fb5d20ee36e48) դեպքում
դեպքում  պարբերական է և ինտեգրելի` ըստ
պարբերական է և ինտեգրելի` ըստ  -ի
-ի ![{\displaystyle x\in \left[{-\pi ;\pi }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32d26fb14f71309a583f8e22474fb5d20ee36e48) միջակայքում, ապա ինտեգրելի կլինի նաև նրանց արտադրյալը`
միջակայքում, ապա ինտեգրելի կլինի նաև նրանց արտադրյալը`
 ,
,
![{\displaystyle \left[{\delta ,\pi }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f5d87b4c91639d829d98229c69ef2c231b08286) հատվածի վրա: Հետևաբար, համաձայն Ռիմանի լեմմայի`
հատվածի վրա: Հետևաբար, համաձայն Ռիմանի լեմմայի`
![{\displaystyle \lim \limits _{n\to \infty }\int \limits _{\delta }^{\pi }{\sin(2n+1){u \over 2}\cdot {{\left[{f(x_{0}+u)+f(x_{0}-u)}\right]} \over {2\sin {u \over 2}}}du}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d328990bea52d9c5e5852c57913b708e521c5e6a) :
:
Թեորեմը ապացուցված է՛: -357-


![{\displaystyle [-\pi \;;\pi \;]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc409c7da7171825e301c33cbf345ea4c61ca42b)














![{\displaystyle S_{n}(x_{0},f)={1 \over \pi }\int \limits _{0}^{\pi }{\sin(2n+1){u \over 2}\cdot {{\left[{f(x_{0}+u)+f(x_{0}-u)}\right]} \over {2\sin {u \over 2}}}du}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b0174bd004d748cea6fd0bd781366bcaf415873)

![{\displaystyle S_{n}(x_{0},f)={1 \over \pi }\int \limits _{0}^{\delta }{\sin(2n+1){u \over 2}\cdot {{\left[{f(x_{0}+u)+f(x_{0}-u)}\right]} \over {2\sin {u \over 2}}}du}+{1 \over \pi }\int \limits _{\delta }^{\pi }{\sin(2n+1){u \over 2}\cdot {{\left[{f(x_{0}+u)+f(x_{0}-u)}\right]} \over {2\sin {u \over 2}}}du}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48079a1d5daa92e5590537d4b9b48726c474fd0e)

![{\displaystyle \left[{\delta ,\pi }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f5d87b4c91639d829d98229c69ef2c231b08286)


![{\displaystyle x\in \left[{-\pi ;\pi }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32d26fb14f71309a583f8e22474fb5d20ee36e48)



![{\displaystyle \lim \limits _{n\to \infty }\int \limits _{\delta }^{\pi }{\sin(2n+1){u \over 2}\cdot {{\left[{f(x_{0}+u)+f(x_{0}-u)}\right]} \over {2\sin {u \over 2}}}du}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d328990bea52d9c5e5852c57913b708e521c5e6a)